6. Diff 算法
6. Diff 算法
无论是哪种 Diff 算法,都遵循同样的处理规则:
- 判断是否有节点需要移动,以及应该如何移动;(可复用的节点)
- 找出那些需要被添加或移除的节点。(其他的节点)
一、简单 Diff
1. 不考虑 dom 复用
const oldChildren = n1.children;
const newChildren = n2.children;
// 旧的一组子节点的长度
const oldLen = oldChildren.length;
// 新的一组子节点的长度
const newLen = newChildren.length;
// 两组子节点的公共长度,即两者中较短的那一组子节点的长度
const commonLength = Math.min(oldLen, newLen);
// 遍历 commonLength 次
for (let i = 0; i < commonLength; i++) {
patch(oldChildren[i], newChildren[i], container);
}
// 如果 newLen > oldLen,说明有新子节点需要挂载
if (newLen > oldLen) {
for (let i = commonLength; i < newLen; i++) {
patch(null, newChildren[i], container);
}
} else if (oldLen > newLen) {
// 如果 oldLen > newLen,说明有旧子节点需要卸载
for (let i = commonLength; i < oldLen; i++) {
unmount(oldChildren[i]);
}
}2. 考虑 dom 复用
在 patch 时,很多时候新旧节点之间存在相同的子节点,二者仅仅是顺序不同,为了提高性能,我们需要复用这些节点,通过 DOM 的移动来完成子节点的更新 。
| 问题 | 回答 |
|---|---|
| 如何确定哪些节点可复用 | 新旧节点中 key 值相同 |
| 如何判断一个节点是否需要移动 | 节点在旧 children 中的索引小于最大索引值 lastIndex |
| 一个节点该移动到哪里 | 新 children 的顺序就是更新后真实 DOM 节点应有的顺序 |
| 如何确定新增节点 | 新节点没有在旧的一组子节点中找到可复用的节点 |
| 如何确定卸载节点 | 遍历完旧的 children 依然存在新 children 中没有的节点 |
const oldChildren = n1.children;
const newChildren = n2.children;
// 用来存储寻找过程中遇到的最大索引值
let lastIndex = 0;
for (let i = 0; i < newChildren.length; i++) {
const newVNode = newChildren[i];
let j = 0;
// 在第一层循环中定义变量 find,代表是否在旧的一组子节点中找到可复用的节点,
// 初始值为 false,代表没找到
let find = false;
for (j; j < oldChildren.length; j++) {
const oldVNode = oldChildren[j];
// 如果找到了具有相同 key 值的两个节点,说明可以复用,但仍然需要调用patch函数更新
if (newVNode.key === oldVNode.key) {
// 一旦找到可复用的节点,则将变量 find 的值设为 true
find = true;
patch(oldVNode, newVNode, container);
// 如果当前找到的节点在旧 children 中的索引小于最大索引值lastIndex,
// 说明该节点对应的真实 DOM 需要移动
if (j < lastIndex) {
// 先获取 newVNode 的前一个 vnode,即 prevVNode
const prevVNode = newChildren[i - 1];
// 如果 prevVNode 不存在,则说明当前 newVNode 是第一个节点,它不需要移动
if (prevVNode) {
// 由于我们要将 newVNode 对应的真实 DOM 移动到prevVNode 对应真实 DOM后面
// 所以我们需要获取 prevVNode 所对应真实 DOM 的下一个兄弟节点,并将其作为锚点
const anchor = prevVNode.el.nextSibling;
// 调用 insert 方法将 newVNode 对应的真实 DOM 插入到锚点元素前面,
// 也就是 prevVNode 对应真实 DOM 的后面
insert(newVNode.el, container, anchor);
}
} else {
// 如果当前找到的节点在旧 children 中的索引不小于最大索引值,
// 则更新 lastIndex 的值
lastIndex = j;
}
break;
}
}
// 如果代码运行到这里,find 仍然为 false,
// 说明当前 newVNode 没有在旧的一组子节点中找到可复用的节点
// 也就是说,当前 newVNode 是新增节点,需要挂载
if (!find) {
// 为了将节点挂载到正确位置,我们需要先获取锚点元素
// 首先获取当前 newVNode 的前一个 vnode 节点
const prevVNode = newChildren[i - 1];
let anchor = null;
if (prevVNode) {
// 如果有前一个 vnode 节点,则使用它的下一个兄弟节点作为锚点元素
anchor = prevVNode.el.nextSibling;
} else {
// 如果没有前一个 vnode 节点,说明即将挂载的新节点是第一个子节点
// 这时我们使用容器元素的 firstChild 作为锚点
anchor = container.firstChild;
}
// 挂载 newVNode
patch(null, newVNode, container, anchor);
}
}
// 遍历旧的一组子节点
for (let i = 0; i < oldChildren.length; i++) {
const oldVNode = oldChildren[i];
// 拿旧子节点 oldVNode 去新的一组子节点中寻找具有相同 key 值的节点
const has = newChildren.find((vnode) => vnode.key === oldVNode.key);
if (!has) {
// 如果没有找到具有相同 key 值的节点,则说明需要删除该节点
// 调用 unmount 函数将其卸载
unmount(oldVNode);
}
}- 如果找到了具有相同 key 值的两个节点,说明可以复用,但仍然需要调用 patch 函数更新,因为新的虚拟节点子节点的内容可能发生改变。
- 移动节点指的是,移动一个虚拟节点所对应的真实 DOM 节点,并不是移动虚拟节点本身。
简单 Diff 算法的核心逻辑是,拿新的一组子节点中的节点去旧的一组子节点中寻找可复用的节点。如果找到了,则记录该节点的位置索引。我们把这个位置索引称为最大索引。在整个更新过程中,如果一 个节点的索引值小于最大索引,则说明该节点对应的真实 DOM 元素需要移动。
二、双端 Diff
1. 简单 Diff 存在的问题
简单 Diff 算法的问题在于,它对 DOM 的移动操作并不是最优的。如下图所示的节点,如果使用简单 Diff 来更新,会发生两次 DOM 移动操作。
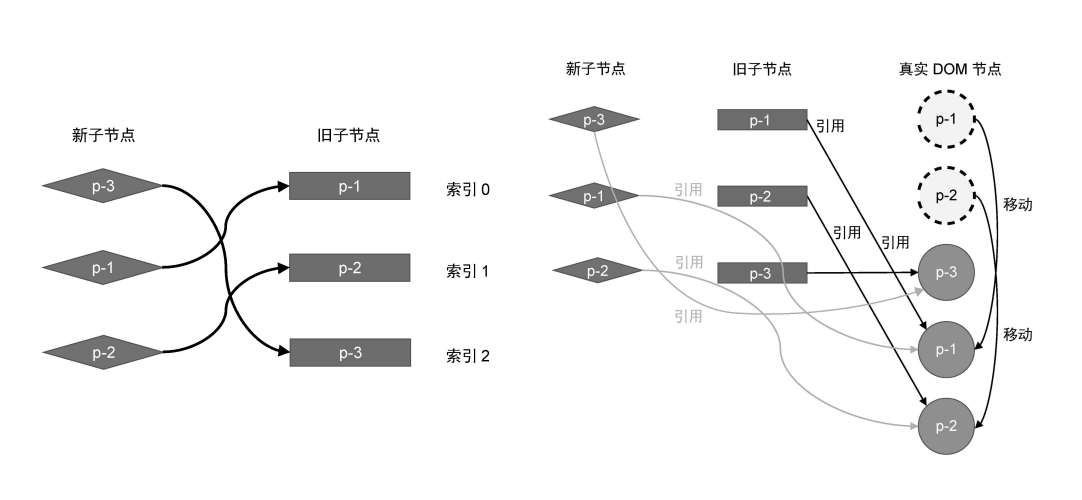
然而我们很容易的可以看出,其实只需要一步 DOM 节点的移动操作就可以完成更新,即只需要把真实 DOM 节点 p-3 移动到真实 DOM 节点 p-1 前面。
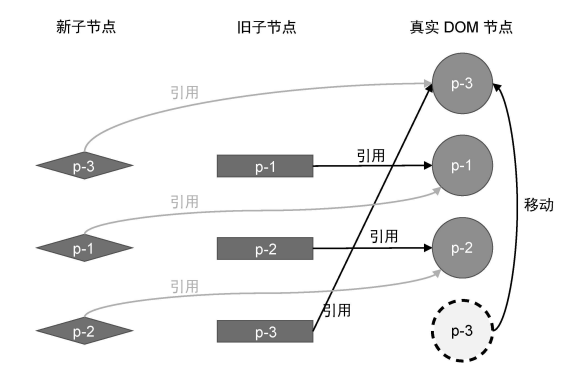
2. 双端 Diff 的理想情况
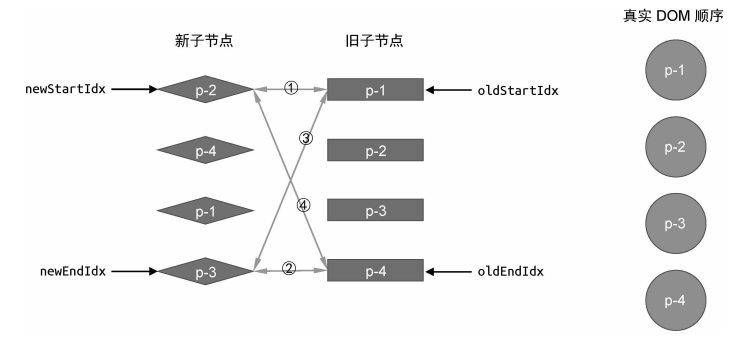
顾名思义,双端 Diff 算法是一种同时对新旧两组子节点的两个端点进行比较的算法。因此我们需要四个索引值,分别指向新旧两组子节点的端点,如图所示。
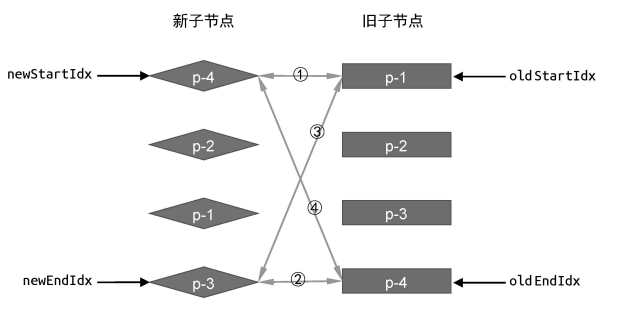
理想情况下假设双端 Diff 算法的每一轮比较都会命中四个步骤中的一种,此时其过程如下图所示
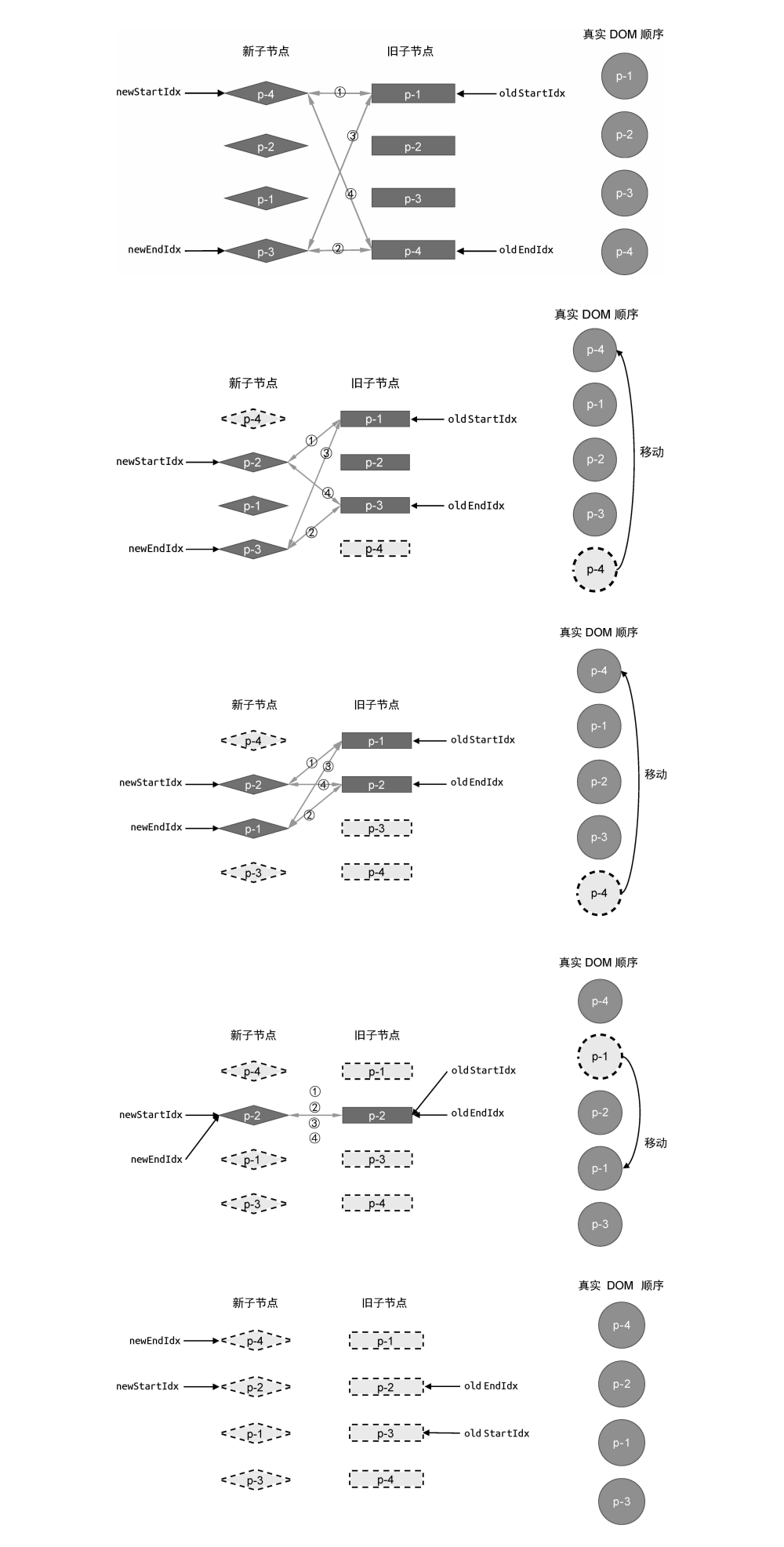
对应的代码实现如下
function patchKeyedChildren(n1, n2, container) {
const oldChildren = n1.children;
const newChildren = n2.children;
// 四个索引值
let oldStartIdx = 0;
let oldEndIdx = oldChildren.length - 1;
let newStartIdx = 0;
let newEndIdx = newChildren.length - 1;
// 四个索引指向的 vnode 节点
let oldStartVNode = oldChildren[oldStartIdx];
let oldEndVNode = oldChildren[oldEndIdx];
let newStartVNode = newChildren[newStartIdx];
let newEndVNode = newChildren[newEndIdx];
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
if (oldStartVNode.key === newStartVNode.key) {
// 第一步:oldStartVNode 和 newStartVNode 比较(不用移动)
// 1. patch
patch(oldStartVNode, newStartVNode, container);
// 2. 更新相关索引,指向下一个位置
oldStartVNode = oldChildren[++oldStartIdx];
newStartVNode = newChildren[++newStartIdx];
} else if (oldEndVNode.key === newEndVNode.key) {
// 第二步:oldEndVNode 和 newEndVNode 比较(不用移动)
patch(oldEndVNode, newEndVNode, container);
oldEndVNode = oldChildren[--oldEndIdx];
newEndVNode = newChildren[--newEndIdx];
} else if (oldStartVNode.key === newEndVNode.key) {
// 第三步:oldStartVNode 和 newEndVNode 比较(需要移动)
patch(oldStartVNode, newEndVNode, container);
// 将oldStartVNode移动到oldEndVNode的后面
insert(oldStartVNode.el, container, oldEndVNode.el.nextSibling);
oldStartVNode = oldChildren[++oldStartIdx];
newEndVNode = newChildren[--newEndIdx];
} else if (oldEndVNode.key === newStartVNode.key) {
// 第四步:oldEndVNode 和 newStartVNode 比较(需要移动)
patch(oldEndVNode, newStartVNode, container);
// oldEndVNode.el 移动到 oldStartVNode.el 前面
insert(oldEndVNode.el, container, oldStartVNode.el);
// 移动 DOM 完成后,更新索引值,并指向下一个位置
oldEndVNode = oldChildren[--oldEndIdx];
newStartVNode = newChildren[++newStartIdx];
}
}
}3. 双端 Diff 的非理想情况
双端 Diff 算法的每一轮比较不一定都会命中四个步骤中的一种,如下图所示,四次比较都不能命中从而进行复用,此时的做法应该是:拿新的一组子节点中的头部节点去旧的一组子节点中寻找,如果存在说明此节点可复用,将其移动到旧子节点首节点的前面;如果没有找到,说明此节点为新增节点,将其挂载到头部。
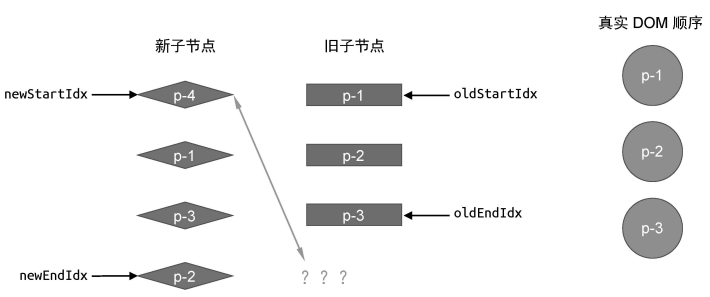
另外还存在一个问题是按照这四个步骤遍历完之后,新旧节点中可能存在还未处理的节点,如果存在新子节点未处理,说明需要对其进行挂载;而存在旧子节点未处理,说明需要对其进行卸载。
function patchKeyedChildren(n1, n2, container) {
const oldChildren = n1.children;
const newChildren = n2.children;
// 四个索引值
let oldStartIdx = 0;
let oldEndIdx = oldChildren.length - 1;
let newStartIdx = 0;
let newEndIdx = newChildren.length - 1;
// 四个索引指向的 vnode 节点
let oldStartVNode = oldChildren[oldStartIdx];
let oldEndVNode = oldChildren[oldEndIdx];
let newStartVNode = newChildren[newStartIdx];
let newEndVNode = newChildren[newEndIdx];
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
// 增加两个判断分支,如果头尾部节点为 undefined,则说明该节点已经被处理过了,直接跳到下一个位置
if (!oldStartVNode) {
oldStartVNode = oldChildren[++oldStartIdx];
} else if (!oldEndVNode) {
oldEndVNode = oldChildren[--oldEndIdx];
} else if (oldStartVNode.key === newStartVNode.key) {
// 省略部分代码
} else if (oldEndVNode.key === newEndVNode.key) {
// 省略部分代码
} else if (oldStartVNode.key === newEndVNode.key) {
// 省略部分代码
} else if (oldEndVNode.key === newStartVNode.key) {
// 省略部分代码
} else {
const idxInOld = oldChildren.findIndex((node) => node.key === newStartVNode.key);
// 1. 存在可复用的节点
if (idxInOld > 0) {
const vnodeToMove = oldChildren[idxInOld];
patch(vnodeToMove, newStartVNode, container);
insert(vnodeToMove.el, container, oldStartVNode.el);
oldChildren[idxInOld] = undefined;
newStartVNode = newChildren[++newStartIdx];
} else {
// 2. 新增节点
// 将 newStartVNode 作为新节点挂载到头部,使用当前头部节点oldStartVNode.el 作为锚点
patch(null, newStartVNode, container, oldStartVNode.el);
}
newStartVNode = newChildren[++newStartIdx];
}
}
// 循环结束后检查索引值的情况,
if (oldEndIdx < oldStartIdx && newStartIdx <= newEndIdx) {
// 如果满足条件,则说明有新的节点遗留,需要挂载它们
// 3. 新增节点
for (let i = newStartIdx; i <= newEndIdx; i++) {
patch(null, newChildren[i], container, oldStartVNode.el);
}
} else if (newEndIdx < newStartIdx && oldStartIdx <= oldEndIdx) {
// 4. 卸载节点(移除操作)
for (let i = oldStartIdx; i <= oldEndIdx; i++) {
unmount(oldChildren[i]);
}
}
}vue2 中使用的就是这种双端 Diff 的算法
三、快速 Diff
1. 特殊情况
快速 Diff 算法借鉴了纯文本 Diff 算法中预处理的步骤,对 Diff 过程两组子节点中 相同的前置和后置节点 优先进行处理,因为这部分前后的相对位置不变,不需要进行移动,只需要在两者之间打补丁即可。
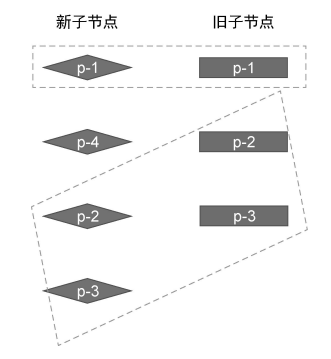
在所有旧子节点处理完毕,而新子节点中还存在未被处理的节点,则这些遗留的节点应该作为新增节点被 挂载 。
在所有新子节点处理完毕,而旧子节点中还存在未被处理的节点,则这些遗留的节点应该被 卸载 。
function patchKeyedChildren(n1, n2, container) {
const newChildren = n2.children;
const oldChildren = n1.children;
// 1. 更新相同的前置节点
let j = 0;
let oldVNode = oldChildren[j];
let newVNode = newChildren[j];
while (oldVNode.key === newVNode.key) {
patch(oldVNode, newVNode, container);
j++;
oldVNode = oldChildren[j];
newVNode = newChildren[j];
}
// 2. 更新相同的后置节点
// 由于新旧两组子节点的数量可能不同,所以我们需要两个索引
let oldEnd = oldChildren.length - 1;
let newEnd = newChildren.length - 1;
oldVNode = oldChildren[oldEnd];
newVNode = newChildren[newEnd];
while (oldVNode.key === newVNode.key) {
patch(oldVNode, newVNode, container);
oldEnd--;
newEnd--;
oldVNode = oldChildren[oldEnd];
newVNode = newChildren[newEnd];
}
// 3. 需被挂载的节点
if (j > oldEnd && j <= newEnd) {
// 锚点的索引
const anchorIndex = newEnd + 1;
// 锚点元素
const anchor = anchorIndex < newChildren.length ? newChildren[anchorIndex].el : null;
// 采用 while 循环,调用 patch 函数逐个挂载新增节点
while (j <= newEnd) {
patch(null, newChildren[j++], container, anchor);
}
}
// 4. 需被卸载的节点
else if (j > newEnd && j <= oldEnd) {
// j -> oldEnd 之间的节点应该被卸载
while (j <= oldEnd) {
unmount(oldChildren[j++]);
}
}
}2. 一般情况处理
在特殊情况下,给出的例子比较理想化,当 处理完相同的前置节点或后置节点后,新旧两组子节点中总会有一组子节点全部被处理完毕。在这种情况下,只需要简单地挂载、卸载节点即可。但一般情况下情况会更加复杂,如图所示:
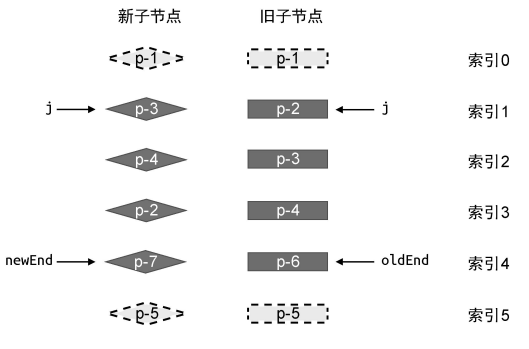
在处理完相同的前置和后置节点之后,剩下的依然是两组子节点序列。按照通用思路思考,接下来需要找出可复用的节点,是否需要移动,移动到什么位置以及需要进行挂载和删除的其他节点。
这里大体的思路是:
构造 source 数组:表示新子节点在旧子节点中的位置索引,长度为新子节点中尚未处理的节点数。
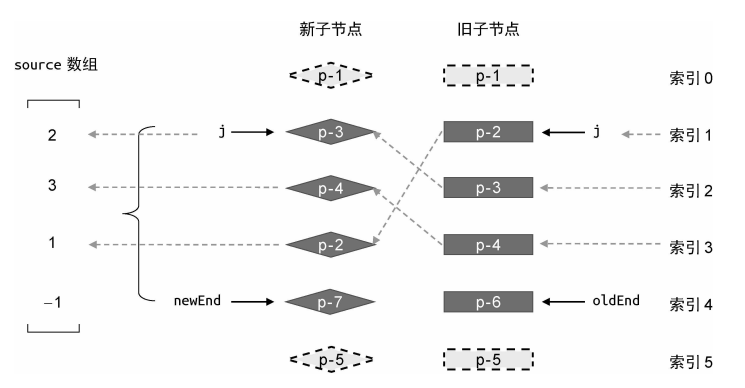
source数组 构造最长递增子序列:依据 source 数组构造最长递增子序列,此序列表示其中节点的相对位置没有发生变化。
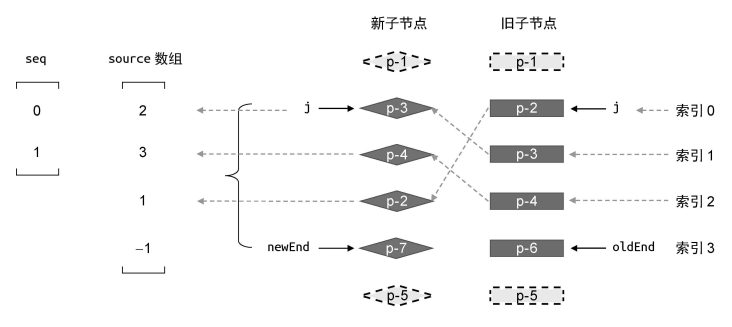
seq为最长递增子序列的索引数组
即找出更新前后顺序没有发生变化的节点,移动剩下的节点从而完成最小的移动次数。
function patchKeyedChildren(n1, n2, container) {
const newChildren = n2.children;
const oldChildren = n1.children;
let j = 0;
let oldVNode = oldChildren[j];
let newVNode = newChildren[j];
while (oldVNode.key === newVNode.key) {
patch(oldVNode, newVNode, container);
j++;
oldVNode = oldChildren[j];
newVNode = newChildren[j];
}
let oldEnd = oldChildren.length - 1;
let newEnd = newChildren.length - 1;
oldVNode = oldChildren[oldEnd];
newVNode = newChildren[newEnd];
while (oldVNode.key === newVNode.key) {
patch(oldVNode, newVNode, container);
oldEnd--;
newEnd--;
oldVNode = oldChildren[oldEnd];
newVNode = newChildren[newEnd];
}
if (j > oldEnd && j <= newEnd) {
const anchorIndex = newEnd + 1;
const anchor = anchorIndex < newChildren.length ? newChildren[anchorIndex].el : null;
while (j <= newEnd) {
patch(null, newChildren[j++], container, anchor);
}
} else if (j > newEnd && j <= oldEnd) {
while (j <= oldEnd) {
unmount(oldChildren[j++]);
}
} else {
// 构造 source 数组
// 长度为新的一组子节点中剩余未处理节点的数量,默认值为-1
const count = newEnd - j + 1;
const source = new Array(count).fill(-1);
在构造 source 数组时,为了提高性能,先遍历新子节点构造出索引表;然后遍历旧子节点根据相同的 key 值可以从索引表中取出对应的节点的索引,从而可以得出新子节点在旧子节点中的位置索引。
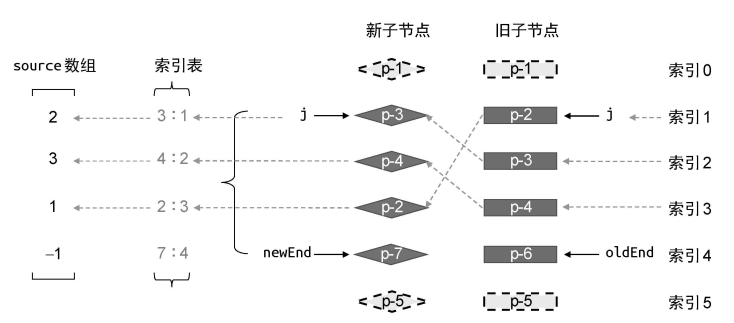
判断是否需要进行移动的方式与简单 Diff 相同——节点在旧 children 中的索引小于最大索引值。
